組合せ回路(Combinational circuit)
組合せ回路は、複数入力の論理演算により一意に決まる回路のことです。単純に定式化しただけでは無駄な回路が多くなるため簡略化が必要です。カルノー図やクワイン・マクラスキー法などの簡略化法が知られていますが、実際の設計現場では論理合成ツールが最適な論理圧縮を自動で行ってくれるため、回路仕様を十分に理解/検討することの方が重要になります。
演習1 7セグメントLEDデコーダ
7セグメントLEDのaセグメントを発光させる論理を作り、その動作の妥当性を確認しなさい。ただし入力4bitのうち10以上の値は入力されないものとする(don't care)。
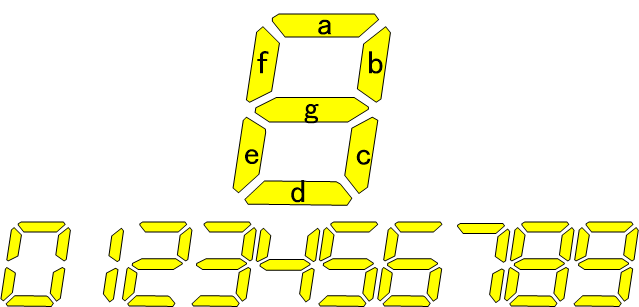
解説
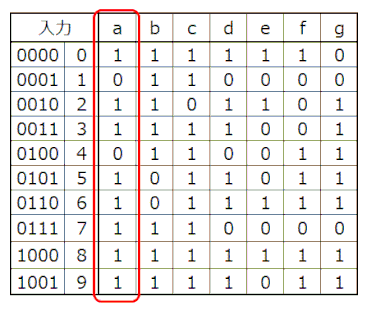
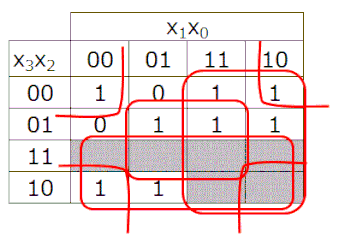
まず真理値表を作成します。続いて、4bitの入力値x3x2x1x0を2bitづつ2つに分けて、4x4の表を作成します。そして各条件に対してaの論理を記載します。ただし、10以上は入力されないのでdon't care(表のグレー箇所)として、カルノー図を完成させます。最終的に4項の積和になりますが、XNORブロックがあるので第3と第4項はまとめ、3項の論理和にします。
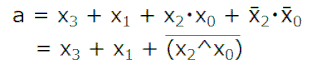
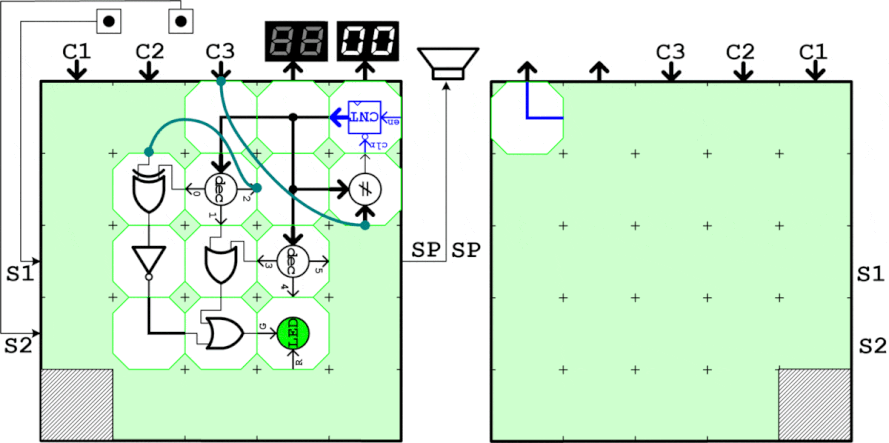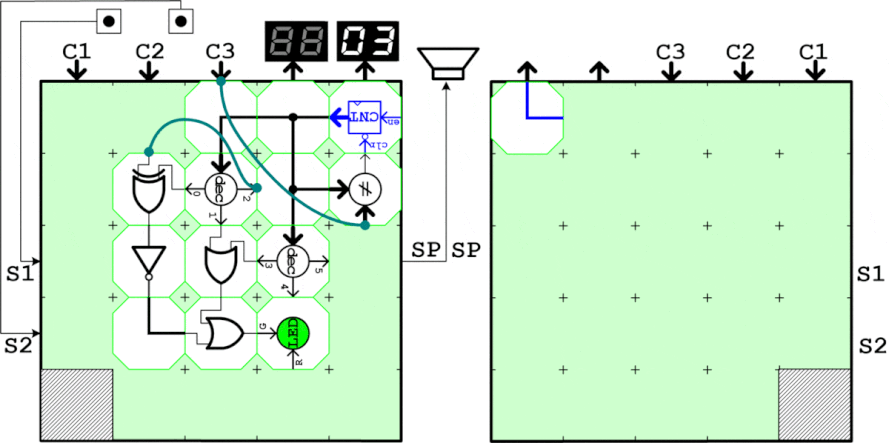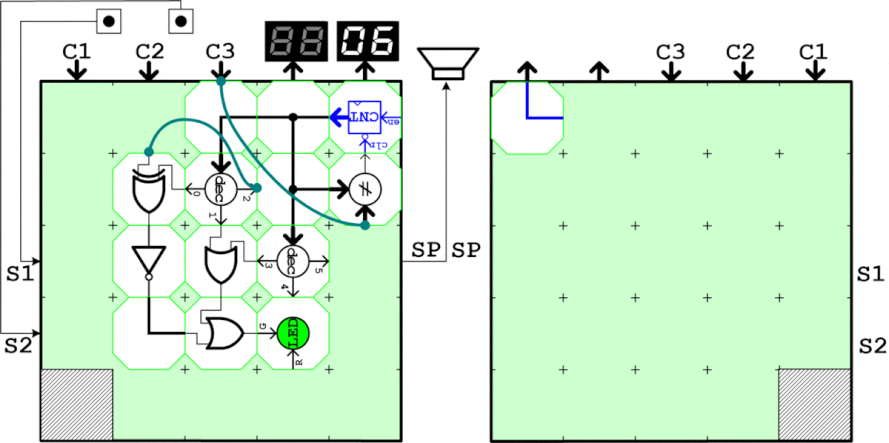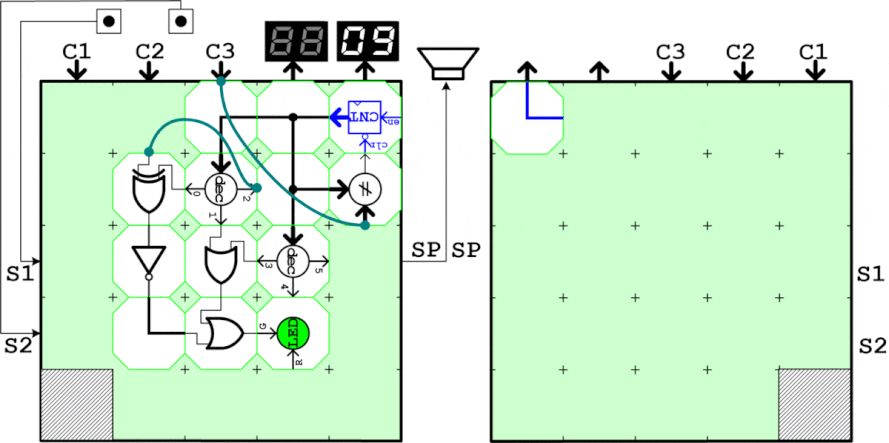
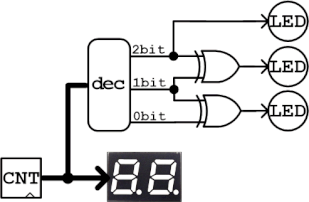
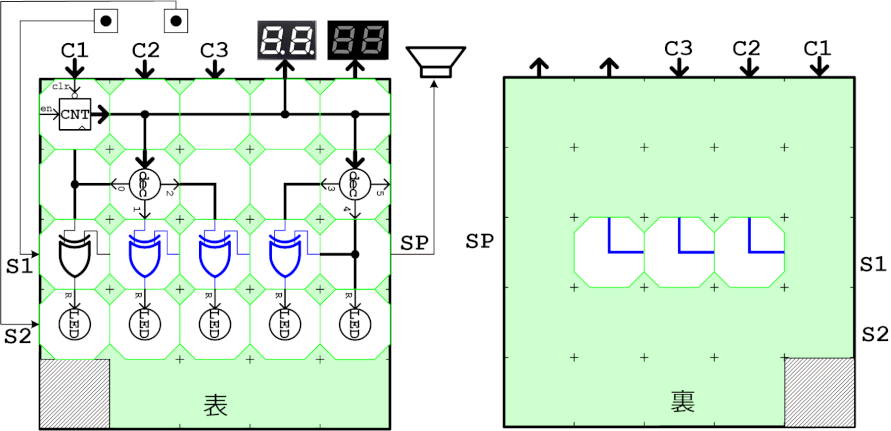
ブロックで動作を確認するために、まず入力の4bitを生成する回路を作ります。0~9までUPしてその次に0に戻るため、カウント値と9を比較してカウントクリアタイミングを生成します。またカウント値は数値表示器で表示し、生成したaはLEDに接続して目視します。カウンタ値が1と4の時にLEDが消灯することを確認すればOK。
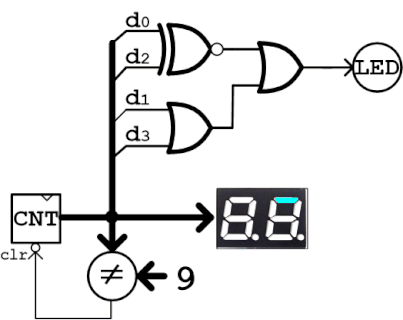
演習2 ハーフアダー/フルアダー/3bit加算器
ハーフアダーとフルアダーの真理値表を作成し、ハーフアダーを使ってフルアダーをブロックで作成し動作を確認しなさい。またフルアダーを3つ使った3bit加算器を図のように組み立てて定数C1とC3の加算が正しく演算されることを確認しなさい。
解説
ハーフアダーの真理値表は右図の通り。
s=a ^ b
c=a・b
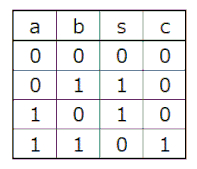
ハーフアダーの真理値表
フルアダーの真理値表は右図の通り。一つ前の桁からのキャリーを入力に持つ点が異なります。ci=0の場合はハーフアダーと等価です。
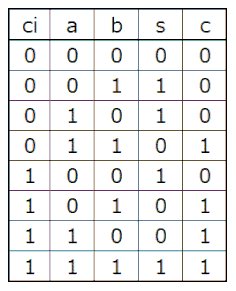
フルアダーの真理値表
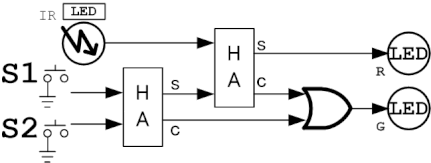
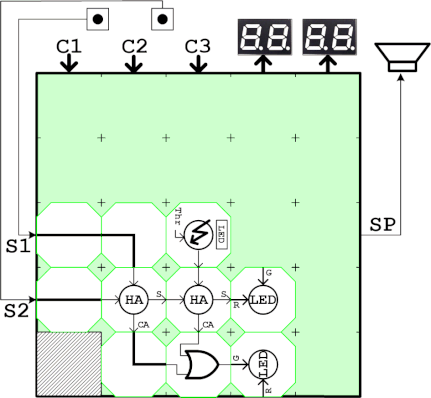
3bit加算器の3bit入力2系統は定数C1とC3に割り当てます。また加算結果はエンコーダーを介して数値表示器に表示させます。基本的にフルアダー3つで構成しますが、LSBのキャリー入力は常に0なので、ハーフアダーと同じになります。c1とc3の値を変更して加算結果が正しく数値表示器に表示されることを確認します。
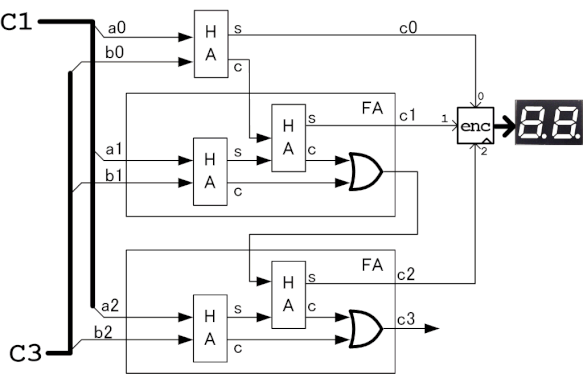
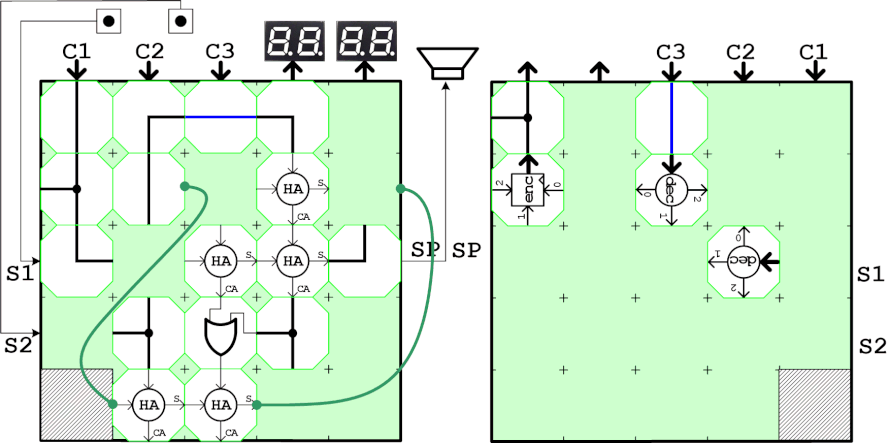
演習3 グレイコードカウンタ
カウンタ出力から3bitのグレイコードを生成する組合せ回路を作成し動作を確認しなさい。
解説
グレイコードは直前のコードとの変化が1bitのみ(ハミング距離が1)となるコードで、ロータリーエンコーダや非同期バス信号の載せ替えなどに応用されます。通常カウンタ出力からXOR演算により簡単に生成することができます。
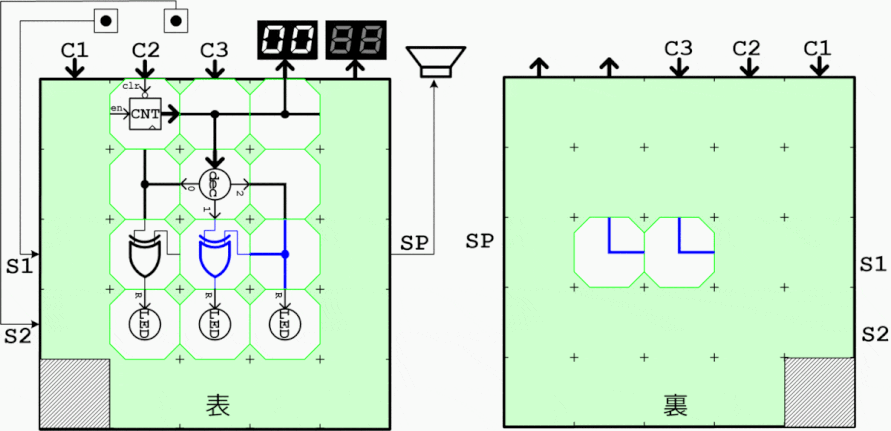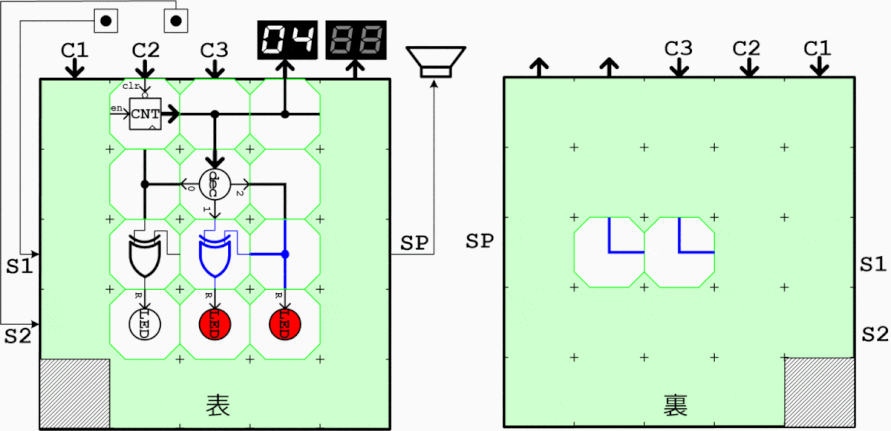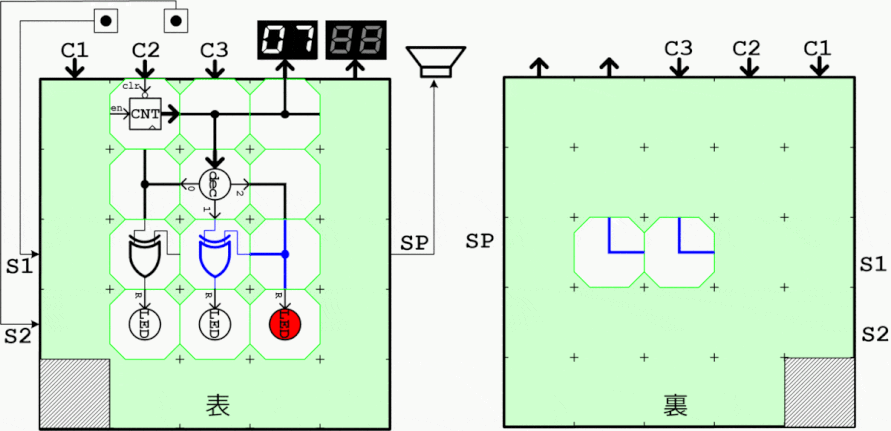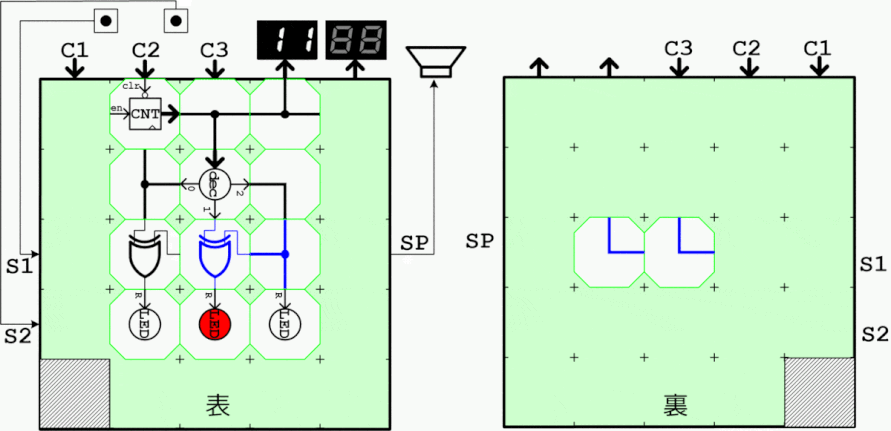
下記は5bitのグレイコード生成用ブロック実装例
お知らせ
■2022/03/03-04 第20回たま工業交流展に出展予定でしたが、展示会自体がコロナのため中止となりました。
■2022/02/01 本店を神奈川県川崎市に移転しました。
■2021/07/19 「プログラミング学習装置」に関する特許が登録されました
■2021/01/20- バーチャル産業交流展に出展しました(1/20-2/19)。
■2020/12/26,27 Cube-D PGを使った「短期プログラミング教室」を開催しました。
■2020/08/25 ネットショップ用ページを追加しました。
■2020/08/11 クラウドファンディングの支援者様にCube-D PGを発送しました。
■2020/08/08 Cube-D PGの全マニュアル(組立、チュートリアル、詳細)を再度更新しました。
■2020/07/21 Cube-D PGの全マニュアル(組立、チュートリアル、詳細)を更新しました。
■2020/07/08 Cube-D PGのロボットカー組立マニュアルがダウンロードできるようになりました。
■2020/06/30 Cube-D PGのチュートリアルマニュアルがダウンロードできるようになりました。
■2020/06/15 「東京技術商店」にてCube-D PGの記事が掲載されました。
■2020/06/11 クラウドファンディング(未来ショッピング)で「Cube-D PG」を公開しました。
■2020/03/28 「プログラミング学習装置」の試作機が完成しました。
■2020/03/04 「プログラミング学習装置」に関する特許を出願しました。
■2019/11/13-15 産業交流展2019に出展しました。
■2019/10/09 ブロックシールPDFがダウンロードできるようになりました。
■2019/09/12 2ブロックだけで作る回路例20を追加しました。
■2019/09/07 Cube-Dを使った論理回路実験室を追加しました。
■2019/09/03 楽天、Yahoo、ヤマダモールでCube-Dとデジタルパペットの販売を開始しました。
■2019/08/09 未来ショッピング公式ストアでCube-Dの販売を開始しました。
■2019/07/19 Makuakeストアからデジタルパペットが購入できるようになりました。
■2019/06/14 デジタルパペットのCFは目標金額の128%で終了しました。ペーパークラフトを公開しました。
■2019/05/22 デジタルパペットの取扱説明書をアップロードしました。
■2019/04/22 Makuake(クラウドファンディング)で「デジタルパペット」を公開しました。
■2019/02/03 アカデミックセット25の一般販売を開始しました(Amazon)。
■2019/01/14 アカデミック版対応操作マニュアル。回路集100をアップロードしました。
■2019/01/14 Cube-D事業を株式会社デジタルキューブに移管しました。

株式会社デジタルキューブ
〒210-0007 神奈川県川崎市川崎区駅前本町11番地2 川崎フロンティアビル4F
電話/FAX 044-813-4547 E-mail info@cube-d.co.jp
