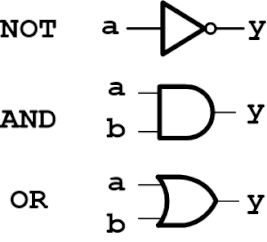
かなり時間が空いてしまいましたが、デジタル回路あるいは論理回路のトピックスを紹介していきたいと思います。Cube-Dをお持ちの方はブロックで実際に回路を組んでいただけると理解が深まると思います。
前回のPWMの話の続きはその中でご紹介する予定です。
今回は演算子のお話です。コンピューターを含む論理回路は、ご存知のように電気信号のOn/Offを2進数で表現してこれを演算子で演算して様々な処理を高速に行います。この演算子として、NOT、AND、ORが基本でこの3つの組み合わせで全ての論理回路を作ることができます。

さてタイトルのNAND演算子は、ANDとNOTの組み合わせです。この演算子が1種類あればNOT、AND、ORが作れてしまいます。すなわち全ての論理回路が作れます。
①NOTを作る

NANDでNOT演算子を作るには入力2本を接続するだけです。NANDの2本の入力を接続するということは2入力の4種類の組み合わせのうちそれぞれ値の同じ2つを使うということです。これがNOTに相当します。

Cube-Dで確認するための実装例を示しておきます。入力はスイッチS1で、出力確認のためにLEDを接続しました。Cube-Dのスイッチはボタンを押すとGND(Lowレベル)になる仕様なので、入力はボタンを押さない場合にHighレベル、押すとLowレベルになります。NANDからNOT演算が実現できていることが確認できます。
②ANDを作る

NANDでAND演算子を作るにはNAND出力を反転すればよいので、①のNOTをNANDの前に配置します。2つのNAND演算子でANDを作ることができます。

Cube-Dで確認するための実装例を示しておきます。入力はスイッチS1とS2で、出力確認のためにLEDを接続します。Cube-Dのスイッチはボタンを押すとGND(Lowレベル)になる仕様なので、入力はボタンを押さない場合にHighレベル、押すとLowレベルになります。2つのスイッチの組み合わせ4通りに対して、AND演算が実現できていることが確認できます。
③ORを作る

NANDからOR演算子を作るにはド・モルガンの法則(AND⇔ORを交換)を応用すれば、NANDの2つの入力を反転すればよいことが分かります。従って、3つのNANDで構成できます。
Cube-Dで確認するための実装例を示しておきます。ブロックは裏面にも配置します(ジャンパ線を使って表面だけでも実装は可能です)。入力はスイッチS1とS2で、出力確認のためにLEDを接続します。Cube-Dのスイッチはボタンを押すとGND(Lowレベル)になる仕様なので、入力はボタンを押さない場合にHighレベル、押すとLowレベルになります。2つのスイッチの組み合わせ4通りに対して、OR演算が実現できていることが確認できます。

表面

裏面
④XORを作る

最後にXOR(排他的論理和)も作ってみます。
y=(a&^b) | (^a&b)から変形してゆくと4つのNANDで作れることが分かります。
Cube-Dで確認するための実装例を示しておきます。ブロックは裏面にも配置します(ジャンパ線を使って表面だけでも実装は可能です)。入力はスイッチS1とS2で、出力確認のためにLEDを接続します。Cube-Dのスイッチはボタンを押すとGND(Lowレベル)になる仕様なので、入力はボタンを押さない場合にHighレベル、押すとLowレベルになります。2つのスイッチの組み合わせ4通りに対して、XOR演算が実現できていることが確認できます。

表面

裏面
今回のNAND演算子は、全ての演算子への置き換えが可能なスーパー演算子という内容でした。昔はANDやORなど演算器が複数入った汎用ロジックICを組み合わせて論理回路を作成していました。確かLS00という型番はNANDが4つ入ったものでした。NOTがLS04番、ANDがLS08番なのになぜNANDが一番若い00番がついていたのか疑問に思った記憶があります。

